Reference
[Paper] [Code] Efficient K-NN for Playlist Continuation (RecSys’18 Challenge)
위의 논문을 바탕으로 KNN 모델을 만들었다.
Process
1. Notaion
- $\mathcal{P}$ : All Playlists in train.json
- $\mathcal{T}$ : All Tracks
- $u$ : Target Playlist in val.json or test.json
- $v$ : Candidate Playlist in train.json
- Known Track $j \in u$
- Candidate Track $i \in v$
- $s_{uv}$ : Similarity between Target Playlist $u$ and Candidate Playlist $v$
- $r_{ui}$ : Relevance between Candidate Track $i$ and Target Playlist $u$
- $k$, $\rho$ : Hyperparameter
2. Similarity $s_{uv}$
2.1 Cosine Similarity
\[\scriptsize{ s_{uv} = \cfrac{\mathbf{u} \cdot \mathbf{v}}{\Vert\mathbf{u}\Vert_2 \Vert\mathbf{v}\Vert_2} }\]OR
\[\scriptsize{ s_{uv} = \sum_{i \in \mathcal{T}} \cfrac{e_{ui}e_{vi}}{\Vert\mathbf{u}\Vert_2 \Vert\mathbf{v}\Vert_2} \text{, where } e_{pi} = \begin{cases} 1 & \text{if track $i$ in playlist $p$} \\ 0 & \text{otherwise} \end{cases} }\]여기서 inner product는 id를 one-hot-encoding했을 때의 값이다.
그러나 knn.py에서는 one-hot-encoding을 사용하지 않고 두 playlist 사이의 교집합의 원소의 개수로 구했다.
Neighbor 모델에서와는 다르게 여기서는 playlist-playlist similarity를 구한다.
2.2 Weighting by Inverse Item Frequency (IDF)
\[\scriptsize{ s_{uv} = \sum_{i \in \mathcal{T}} ((f_i - 1)^\rho + 1)^{-1} \cdot \cfrac{e_{ui}e_{vi}}{\Vert\mathbf{u}\Vert_2 \Vert\mathbf{v}\Vert_2} }\]where $f_i$ denotes the number of playlists containing track i and $rho$ is an hyperparameter.
Two playlists are more likely similar if they include the same low popularity tracks than if they share tracks that a very large number of other lists also include.
IDF를 사용했을 때 사용하지 않을 때보다 훨씬 성능이 좋았다.
논문에서는 $\rho = 0.4$를 사용해서 같은 $\rho$ 값을 사용하였다.
3. Relevance $r_{ui}$
\[\scriptsize{ r_{ui} = \cfrac{\sum_{v \in N_k(u)} s_{uv} \cdot e_{vi}}{\sum_{v \in N_k(u)} s_{uv}} }\]where $N_k(u)$ is the set of $k$ playlists most similar to $u$.
target playlist $u$에 대해 모든 playlist $v \in \mathcal{P}$와 similarity $s_{uv}$를 구한 다음 가장 similarity가 큰 상위 $k$로 $N_k(u)$를 정한다.
그 $N_k(u)$를 사용해서 playlist-track relevance를 구한다.
Modeling
Input & Output
논문에서는 Song → Song (Tag → Tag)의 방법이지만 이와 같은 input & output은 성능이 더 좋았던 Neighbor 모델을 사용했다.
Neighbor에서 설명했듯이 Neighbor 모델은 한계가 있어서 이 점을 보완하기 위해 KNN 모델에서는 다음과 같은 예측 방식을 따른다.
- Song → Tag
- Tag → Song
즉,
- song only인 경우에 대해 song similarity 기반으로 유사한 playlist를 찾는다. 유사한 playlist에 있는 태그를 자주 등장한 순서대로 정렬한다.
- tag only인 경우에 대해 tag similarity 기반으로 유사한 playlist를 찾는다. 유사한 playlist에 있는 노래에 대해 relevance를 구해서 정렬한다.
similarity를 구할 때 val.json (test.json)에 있는 song / tag와 Neighbor 모델의 예측 결과로 나온 pred song / tag를 사용한다.
각 데이터셋에 대해 similarity를 각각 구하고 더하는데, 더할 때의 가중치도 hyperparameter로 설정하였다.
- $\scriptsize{0 \le \text{(weight_val_songs)} \le 1}$ (wvs)
- weight_pred_songs = 1 - weight_val_songs
- $\scriptsize{0 \le \text{(weight_val_tags)} \le 1}$ (wvt)
- weight_pred_tags = 1 - weight_val_tags
추가적으로,
- similarity를 구할 때 normalize 여부를 달리해서도 사용해봤다.
- 모델의 결과가 song 100개 tag 10개 미만이 되는 경우가 있어서 $k$를 늘릴 수 있는 step을 추가했다.
Optimization
| hyperparameter | optimal value |
|---|---|
| song $k$ | 500 |
| tag $k$ | 90 |
| song step | 50 |
| tag step | 10 |
| sim song | IDF |
| sim tag | IDF |
| sim norm | True |
| wvs | 0.9 |
| wvt | 0.7 |
아래에서 사용한 similarity 종류는 IDF, wvs = 0.9, wvt = 0.7이다.
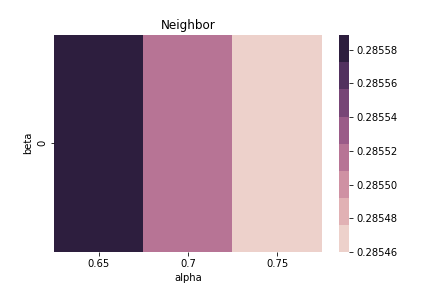
$\alpha = 0.7$ & $\beta = 0.0$ & sim norm = False
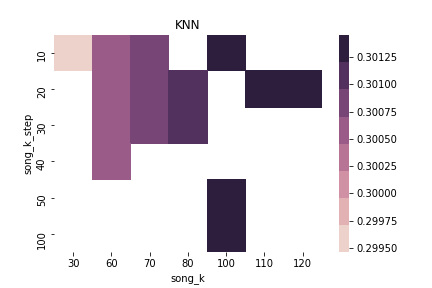
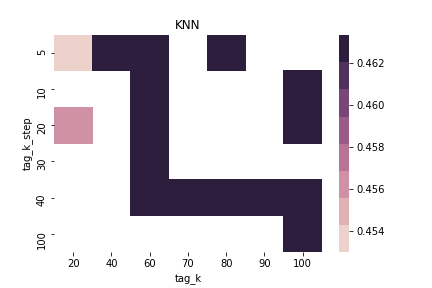
$\alpha = 0.7$ & $\beta = 0.0$ & sim norm = True
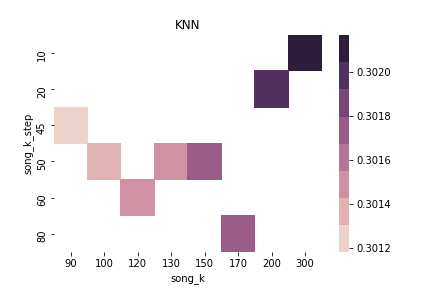
$\alpha = 0.7$ & $\beta = 0.0$ & sim norm = False & using Threshold
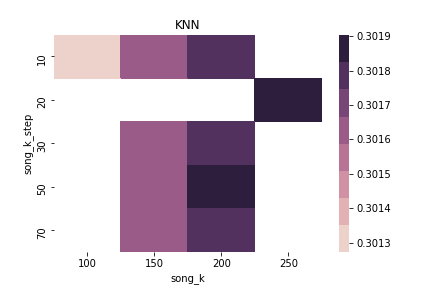
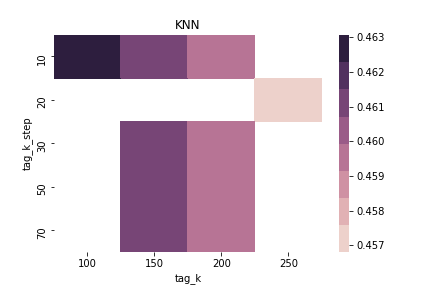
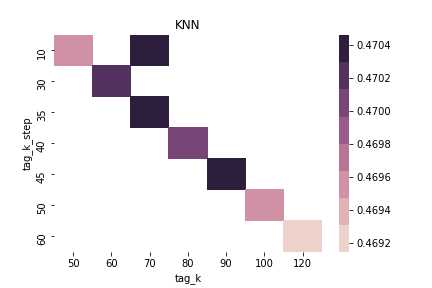
$\alpha = 0.65$ & $\beta = 0.0$ & sim norm = True & using Threshold

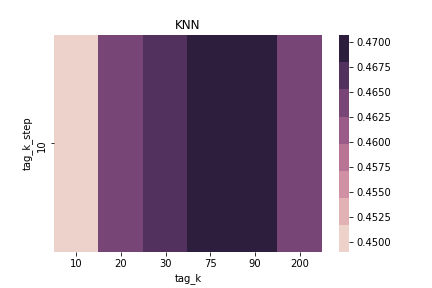
song $k$ = 100 & tag $k$ = 100 & song step = 10 & tag step = 10
Code
KNN.py
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
import numpy as np
import pandas as pd
from collections import Counter
from data_util import tag_id_meta
class KNN:
'''
K Nearest Neighbor
'''
__version__ = "KNN-2.0"
def __init__(self, song_k, tag_k, rho=0.4, \
song_k_step=50, tag_k_step=10, \
weight_val_songs=0.5, weight_pred_songs=0.5, \
weight_val_tags=0.5, weight_pred_tags=0.5, \
sim_songs="idf", sim_tags="idf", sim_normalize=False, \
train=None, val=None, song_meta=None, pred=None):
'''
song_k, tag_k, song_k_step, tag_k_step : int
rho : float; 0.4(default) only for idf
weights : float
sim_songs, sim_tags : "idf"(default), "cos"
sim_normalize : boolean;
'''
### data sets
self.train_id = train["id"].copy()
self.train_songs = train["songs"].copy()
self.train_tags = train["tags"].copy()
self.val_id = val["id"].copy()
self.val_songs = val["songs"].copy()
self.val_tags = val["tags"].copy()
self.val_updt_date = val["updt_date"].copy()
self.song_meta_issue_date = song_meta["issue_date"].copy().astype(np.int64)
self.pred_songs = pred["songs"].copy()
self.pred_tags = pred["tags"].copy()
self.freq_songs = None
self.freq_tags = None
self.song_k = song_k
self.tag_k = tag_k
self.song_k_step = song_k_step
self.tag_k_step = tag_k_step
self.rho = rho
self.weight_val_songs = weight_val_songs
self.weight_pred_songs = weight_pred_songs
self.weight_val_tags = weight_val_tags
self.weight_pred_tags = weight_pred_tags
self.sim_songs = sim_songs
self.sim_tags = sim_tags
self.sim_normalize = sim_normalize
self.__version__ = KNN.__version__
_, id_to_tag = tag_id_meta(train, val)
TOTAL_SONGS = song_meta.shape[0] # total number of songs
TOTAL_TAGS = len(id_to_tag) # total number of tags
### transform date format in val
for idx in self.val_id.index:
self.val_updt_date.at[idx] = int(''.join(self.val_updt_date[idx].split()[0].split('-')))
self.val_updt_date.astype(np.int64)
if self.sim_songs == "idf":
self.freq_songs = np.zeros(TOTAL_SONGS, dtype=np.int64)
for _songs in self.train_songs:
self.freq_songs[_songs] += 1
if self.sim_tags == "idf":
self.freq_tags = np.zeros(TOTAL_TAGS, dtype=np.int64)
for _tags in self.train_tags:
self.freq_tags[_tags] += 1
del train, val, song_meta, pred
def predict(self):
'''
@returns : pandas.DataFrame; columns=['id', 'songs', 'tags']
'''
_range = range(self.val_id.size)
pred = []
all_songs = [set(songs) for songs in self.train_songs] # list of set
all_tags = [set(tags) for tags in self.train_tags] # list of set
for uth in _range:
# predict songs by tags
if self.val_songs[uth] == [] and self.val_tags[uth] != []:
playlist_tags_in_pred = set(self.pred_tags[uth])
playlist_tags_in_val = set(self.val_tags[uth])
playlist_updt_date = self.val_updt_date[uth]
simTags_in_pred = np.array([self._sim(playlist_tags_in_pred, vplaylist, self.sim_tags, opt='tags') for vplaylist in all_tags])
simTags_in_val = np.array([self._sim(playlist_tags_in_val , vplaylist, self.sim_tags, opt='tags') for vplaylist in all_tags])
simTags = ((self.weight_pred_tags * simTags_in_pred) / (len(playlist_tags_in_pred))) + \
((self.weight_val_tags * simTags_in_val) / (len(playlist_tags_in_val)))
songs = set()
try:
song_k = min(len(simTags[simTags > 0]), self.song_k)
except:
song_k = self.song_k
while len(songs) < 100:
top = simTags.argsort()[-song_k:]
_songs = []
for vth in top:
_songs += self.train_songs[vth]
songs = set(_songs)
# check if issue_date of songs is earlier than updt_date of playlist
date_checked = []
for track_i in songs:
if self.song_meta_issue_date[track_i] <= playlist_updt_date:
date_checked.append(track_i)
songs = set(date_checked)
song_k += self.song_k_step
norm = simTags[top].sum()
if norm == 0:
norm = 1.0e+10 # FIXME
relevance = np.array([(song, np.sum([simTags[vth] if song in all_songs[vth] else 0 for vth in top]) / norm) for song in songs])
relevance = relevance[relevance[:, 1].argsort()][-100:][::-1]
pred_songs = relevance[:, 0].astype(np.int64).tolist()
pred.append({
"id" : int(self.val_id[uth]),
"songs" : pred_songs,
"tags" : self.pred_tags[uth]
})
# predict tags using songs
elif self.val_songs[uth] != [] and self.val_tags[uth] == []:
playlist_songs_in_pred = set(self.pred_songs[uth])
playlist_songs_in_val = set(self.val_songs[uth])
simSongs_in_pred = np.array([self._sim(playlist_songs_in_pred, vplaylist, self.sim_songs, opt='songs') for vplaylist in all_songs])
simSongs_in_val = np.array([self._sim(playlist_songs_in_val , vplaylist, self.sim_songs, opt='songs') for vplaylist in all_songs])
simSongs = ((self.weight_pred_songs * simSongs_in_pred) / (len(playlist_songs_in_pred))) + \
((self.weight_val_songs * simSongs_in_val) / (len(playlist_songs_in_val)))
tags = []
try:
tag_k = min(len(simSongs[simSongs > 0]), self.tag_k)
except:
tag_k = self.tag_k
while len(tags) < 10:
top = simSongs.argsort()[-tag_k:]
_tags = []
for vth in top:
_tags += self.train_tags[vth]
counts = Counter(_tags).most_common(30)
tags = [tag for tag, _ in counts]
tag_k += self.tag_k_step
pred_tags = tags[:10]
pred.append({
"id" : int(self.val_id[uth]),
"songs" : self.pred_songs[uth],
"tags" : pred_tags
})
# if val.songs[uth] == [] and val.tags[uth] == [] -> pred.songs[uth] == [] and pred.tags[uth] == []
# if val.songs[uth] != [] and val.tags[uth] != [] -> pred.songs[uth] != [] and pred.tags[uth] != []
else:
pred.append({
"id" : int(self.val_id[uth]),
"songs" : self.pred_songs[uth],
"tags" : self.pred_tags[uth]
})
return pd.DataFrame(pred)
def _sim(self, u, v, sim, opt):
'''
u : set (playlist in train data)
v : set (playlist in test data)
sim : string; "cos", "idf"
opt : string; "songs", "tags"
'''
if sim == "cos":
if self.sim_normalize:
try:
return len(u & v) / ((len(u) ** 0.5) * (len(v) ** 0.5))
except:
return 0
else:
return len(u & v)
elif sim == "idf":
if opt == "songs":
freq = self.freq_songs
elif opt == "tags":
freq = self.freq_tags
freq = freq[list(u & v)]
freq = 1 / (((freq - 1) ** self.rho) + 1) # numpy!
if self.sim_normalize:
try:
return freq.sum() / ((len(u) ** 0.5) * (len(v) ** 0.5))
except:
return 0
else:
return freq.sum()
More Ideas
- IDF 식에서 $((f_i - 1)^\rho + 1)^{-1}$ 부분 변형하기
- optimal $\rho$ 찾기